Soon after Sir Isaac Newton discovered the law of gravitation—which provided a mathematical explanation for why objects fall to Earth and why planets orbit the Sun—he expressed his unease with the idea that one object could exert a force on another far away without any intervening mechanism. This notion, later called “action at a distance,” was philosophically troubling, but it was widely accepted because it worked. Newton’s law was so successful that it even led to the discovery of new planets and allowed astronomers to predict the precise paths of celestial bodies.

Almost a century later, when most questions about gravity had been settled, physicists across Europe turned their attention to a striking discovery made by the Danish physicist Hans Ørsted.

Ørsted's accidental discovery

Ørsted, while preparing a classroom demonstration on electrical phenomena, stumbled upon a perplexing observation. Each time he switched the current on and off in his circuit, a magnetic compass lying nearby would twitch. The compass, placed there by chance and without contact with the circuit, nevertheless responded every time the current changed.

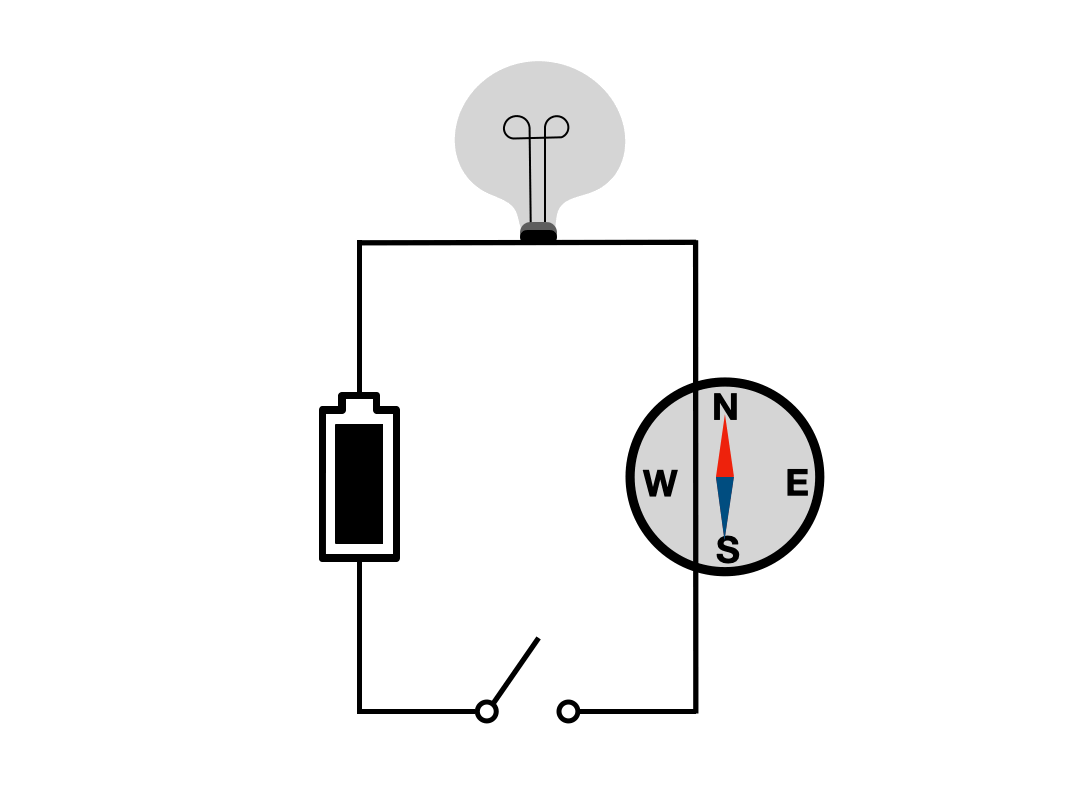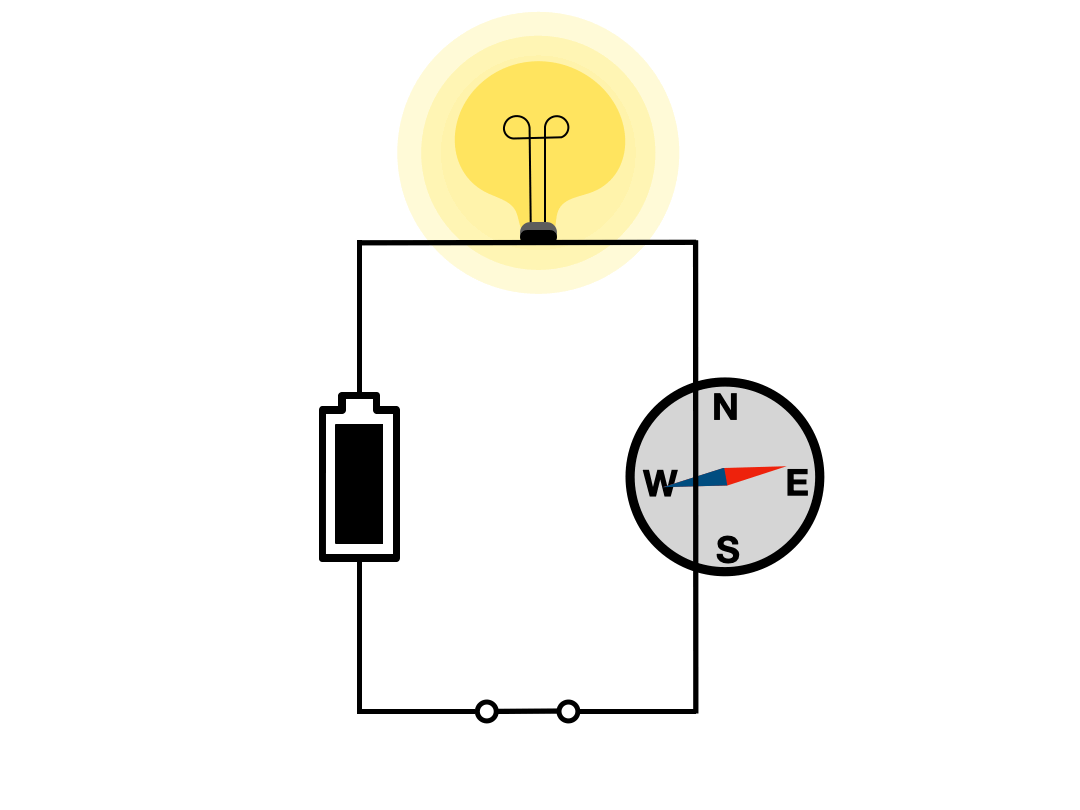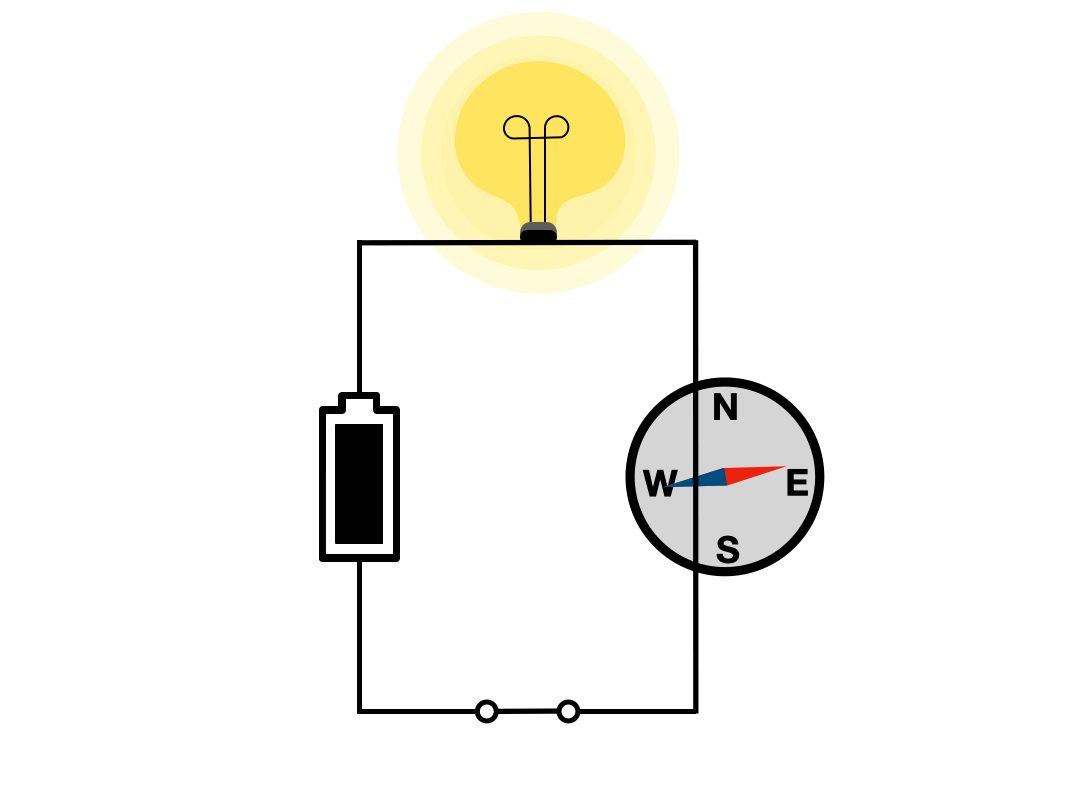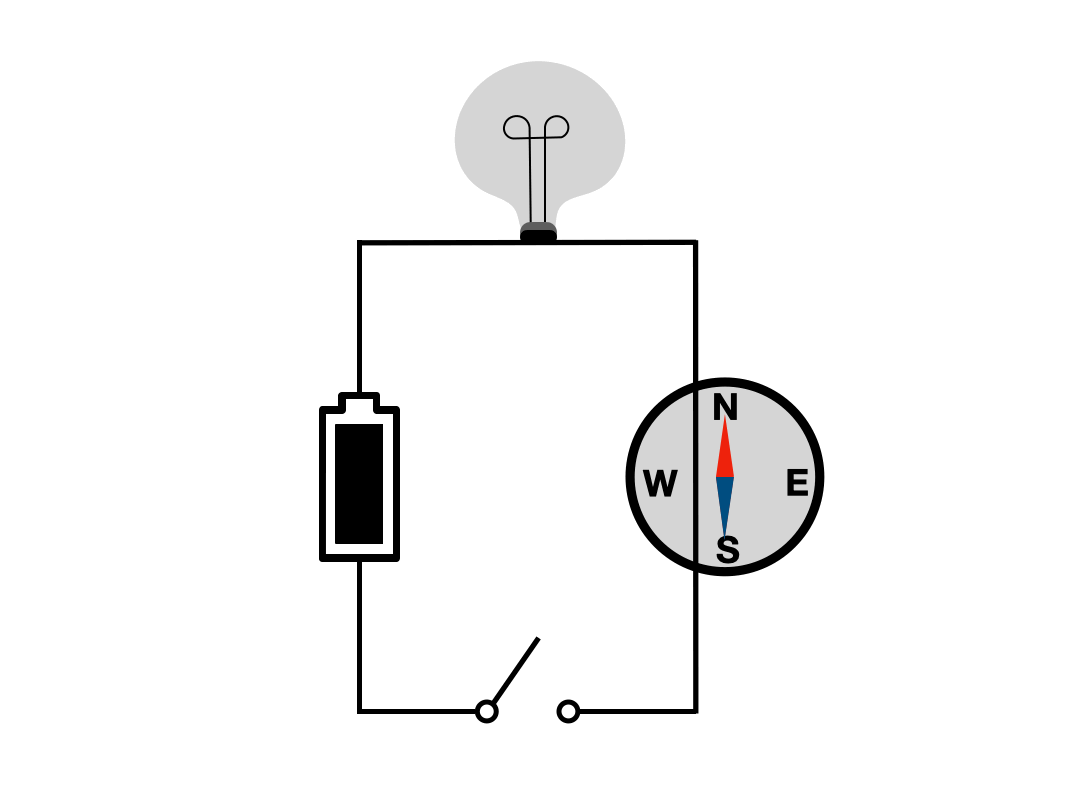
This observation set off a wave of excitement among physicists across Europe. They rushed to replicate the experiment and to search for an explanation. Many were satisfied with the “action at a distance” idea—that somehow the changing current disturbed the nearby needle—though the mysterious connection between electricity and magnetism remained unexplained.

Enter Ampère

Among those captivated was André-Marie Ampère, a French mathematician already known for his work in probability theory. He began conducting his own experiments with suspended coils and magnets, while simultaneously attempting to formulate a theoretical explanation. At first, his hasty efforts created more confusion than clarity. His experimental clumsiness even prompted Laplace to remark: “Monsieur Ampère is so clumsy that when his apparatus does not move, he reportedly pushes to shift it.”

Yet with time, persistence paid off. Ampère performed a series of experiments, most notably with two parallel wires carrying current side by side. He observed that the wires attracted each other when the currents flowed in the same direction but repelled when the currents flowed in opposite directions. Unlike most of his contemporaries, Ampère did not rely solely on the “action at a distance” explanation. Instead, he sought a systematic theory of forces between currents—an approach that laid the groundwork for what would later be described in terms of magnetic fields by Michael Faraday and James Clerk Maxwell.

The magnetic field

In modern terms, a magnetic field is a region of space where moving charges experience a magnetic force. For instance, a charged particle entering such a region is deflected from its straight path and begins spiraling along a helix. One can imagine a magnetic field enveloping a bar magnet. Ampère suggested that a similar influence surrounds a current-carrying wire.

At first, his proposal was dismissed by many contemporaries as an unnecessary complication. They preferred Coulomb’s theory of magnetism, which held that magnets contained two “magnetic fluids”—a north fluid and a south fluid—that produced poles at opposite ends. For them, action at a distance was sufficient to explain why one current-carrying wire exerted a force on another.

Circulating fields

Over time, however, Ampère’s theory prevailed. He proposed that a current-carrying wire generates a circulating magnetic influence around it, which in turn exerts a force on a nearby wire. Measurements confirmed his predictions with remarkable precision, and his conclusion came to be known as Ampère’s circuital law.

Action at a distance has since been shown to be invalid. No object can instantly influence another at a distance. According to Einstein’s special relativity, no information can travel faster than the speed of light in vacuum. Thus, if current begins flowing through one of the wires in Ampère’s setup, the second wire will feel a force only after a time delay equal to the time light takes to travel from the first wire to the second.

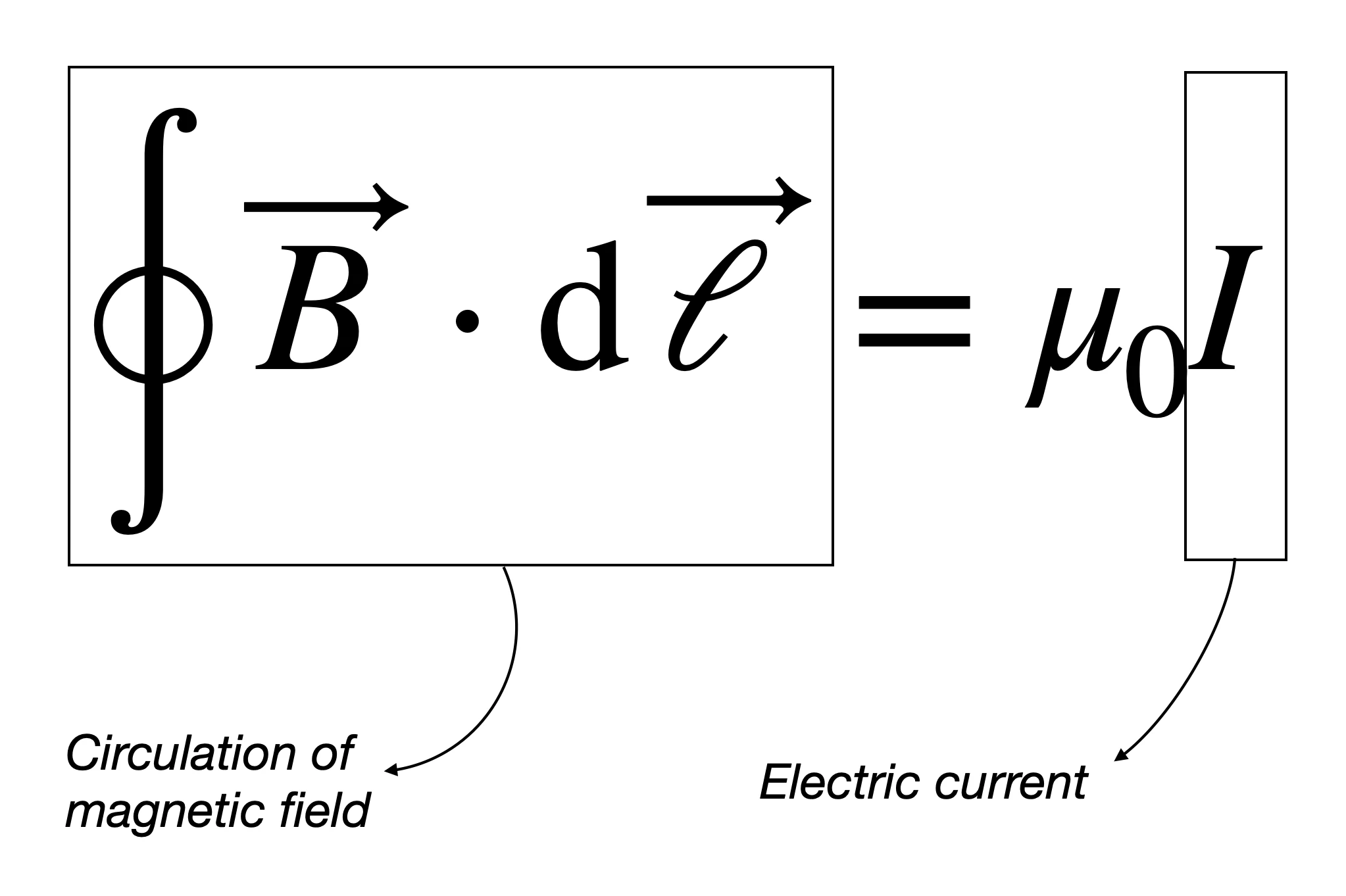
In modern notation, Ampère’s law states that the circulation of the magnetic field around any closed loop (left hand side of the above equation) depends on the total current passing through that loop (the right hand side). To apply the law, we imagine a closed loop around a current-carrying wire, calculate the circulation of the magnetic field, and equate it to the enclosed current. The greater the current, the stronger the circulation of the magnetic field.

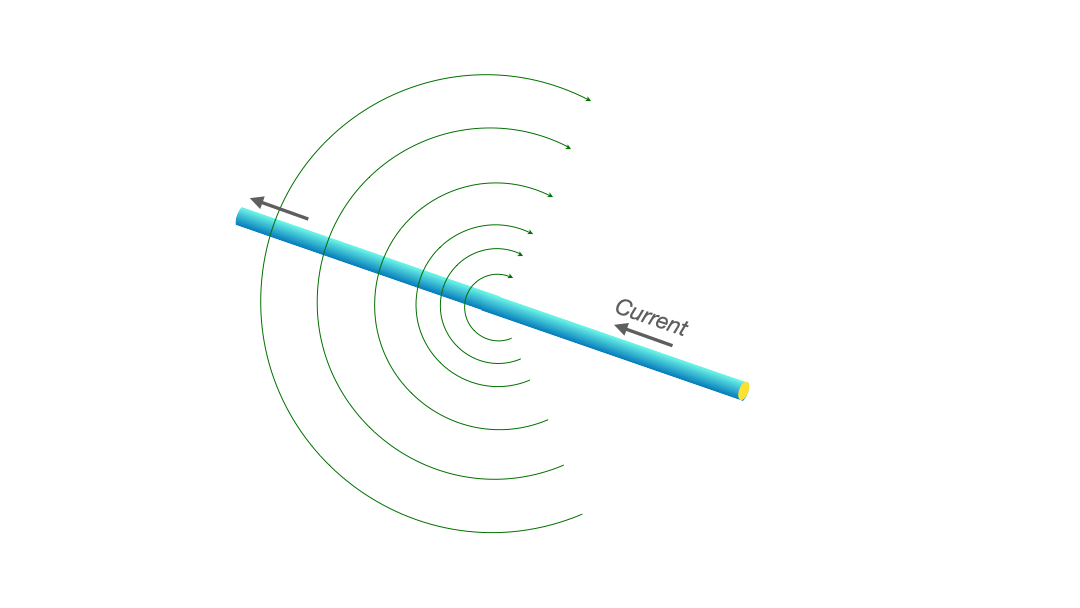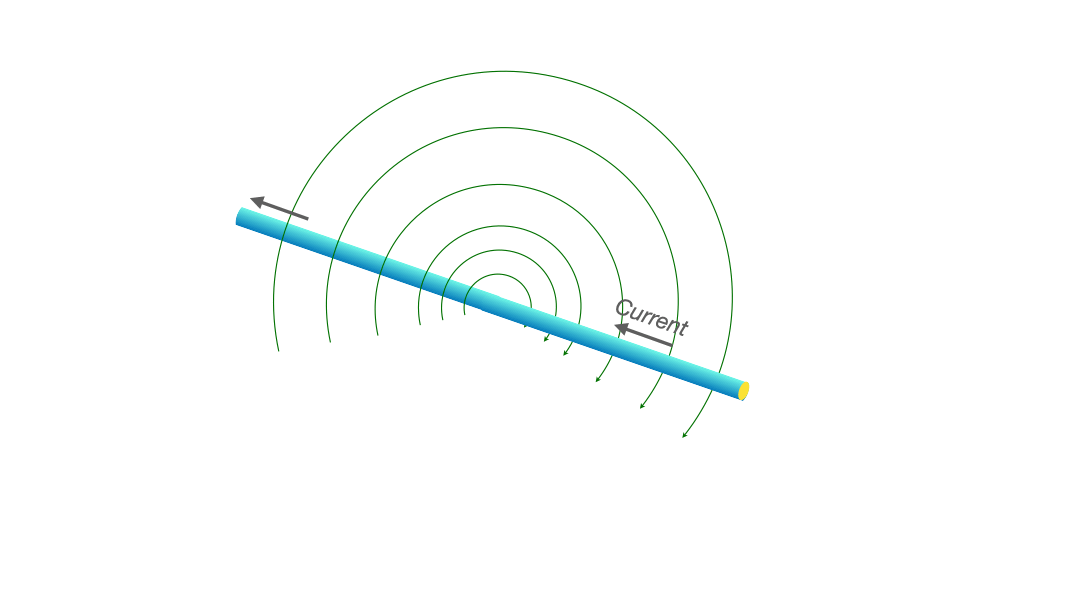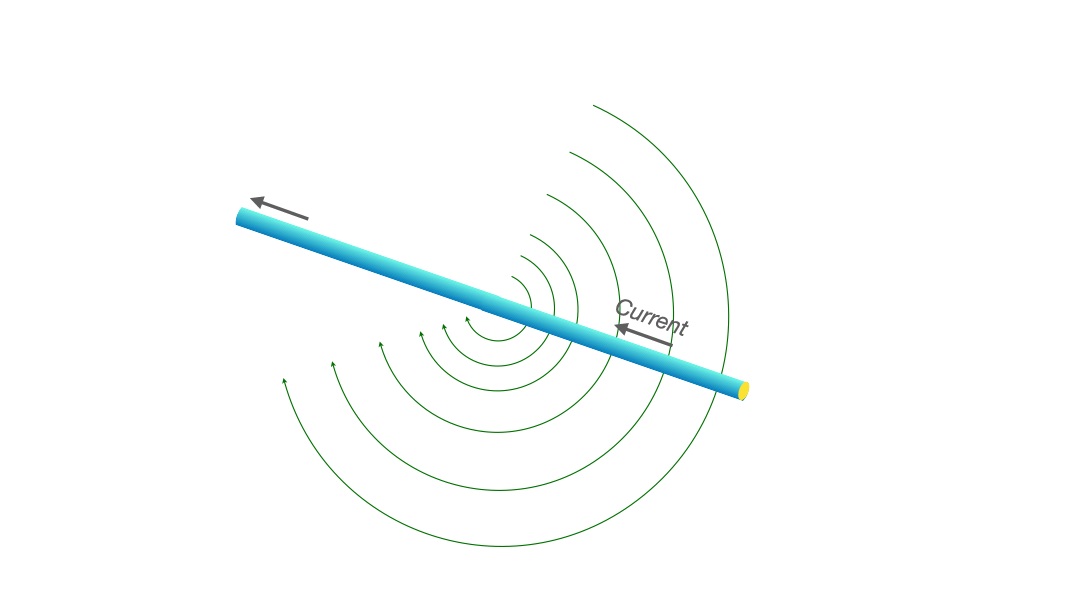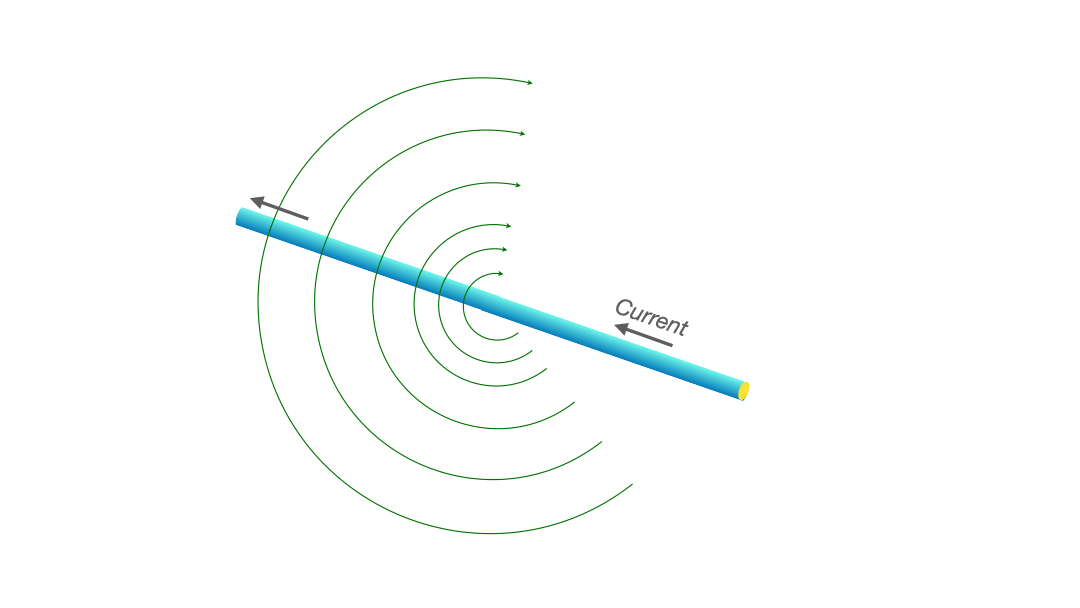
One might picture it this way: just as a tornado stirs the air into circular motion around its eye, a current-carrying wire stirs up the space around it, producing what we call the magnetic field.

Farsightedness of Monsieur Ampère

Ampère—hailed by James Clerk Maxwell as the “Newton of electricity”—was ahead of his time. He conjectured that if currents generate magnetic fields, then even the fields produced by permanent magnets must arise from electric currents within them. Today we know this to be true: all matter is made of atoms, and electrons themselves behave like tiny magnets. Their intrinsic spin and their motion within atomic orbitals both act like circulating currents, producing magnetic fields. In magnets, many of these atomic-scale fields align, reinforcing one another. In non-magnetic substances such as wood, they cancel out due to lack of alignment.

Ampère’s law now stands as one of the cornerstones of electromagnetism, a theory that underpins phenomena ranging from the lightning in the sky to the lights that illuminate our homes and streets at night.