Any gas can be made to glow if a sufficiently high voltage is applied across it. Consider glowing neon signs—the red-orange glow is simply a result of a voltage applied to neon gas within the tubes. If you’re curious about the precise reasons behind this glow, examine the emitted light closely. At first glance, the reddish-orange glow suggests that the light is a combination of shades of both red and orange colours. However, upon closely observing the light after separating it into its constituent colours using a diffraction grating, you’ll notice lines of specific colours in the spectrum separated by darkness. It’s natural to wonder at this point why these particular colours are emitted instead of others.

It becomes even more intriguing when you realise that all neon signs emit the exact same spectrum, hinting that the spectrum is somehow linked to a intrinsic property of neon gas itself. Further, when the same observations are repeated with other gases, it’s observed that different gases produce distinct combinations of colour bands in their spectra, with no two patterns repeating. Thus, these spectra act like fingerprints of specific gases, allowing one to determine the gas responsible simply by examining its spectrum. This uniqueness suggests the spectra reveal something profound about the nature of the gas.
The Link to atoms
If gases are assumed to consist of atoms, their spectra must result from a unique behaviour of those atoms. One can imagine that even a single atom of the gas could produce the entire spectrum, albeit of an extremely faint intensity. It takes the collective identical emission of billions of identical gas atoms to produce the intense bands of colours visible in the final spectrum. Hence analyzing the spectrum can reveal a lot about what could be happening inside each atom of the gas, possibly leading us to understand atomic structure.
Such was the motivation of early 20th-century physicists seeking to understand the atom. By 1911, based on the results of his ingenious experiments, Ernest Rutherford had proposed a simple atomic model resembling the solar system: a tiny, positively charged nucleus surrounded by orbiting electrons, like planets around the Sun. The electrons had to be in motion, or they would plummet directly into the nucleus due to the electrical forces. However, this model had a serious flaw: according to the established laws of electromagnetism, a circling electron should continuously radiate light, resulting in an energy loss and an inward spiral. This would mean that all atoms are inherently unstable and would collapse almost instantly. Clearly, this isn’t the case; otherwise, everything around us would have ceased to exist long ago.
Enter Bohr

All attempts to reconcile the atomic structure with electromagnetism had failed. There was a need for a radical shift in our understanding of the atom. This is when Danish physicist Neils Bohr, a former student of Rutherford, decided to clearly state the conflict rather than attempt to resolve it. Instead of explaining why orbiting electrons don't radiate and spiral into the nucleus, he simply assumed that they don’t. Bohr’s genius lay in recognizing that the theory of electromagnetism, which had been incredibly successful, might have reached its limits within the atom, where it may no longer apply. Instead of forcefully trying to fit the theory into the atomic structure, he elegantly admitted its limitations.
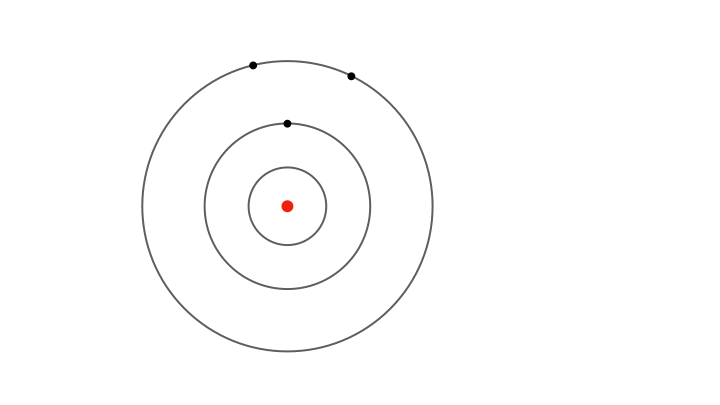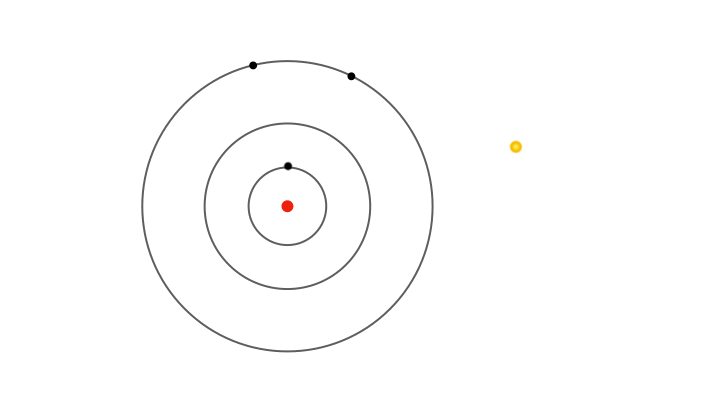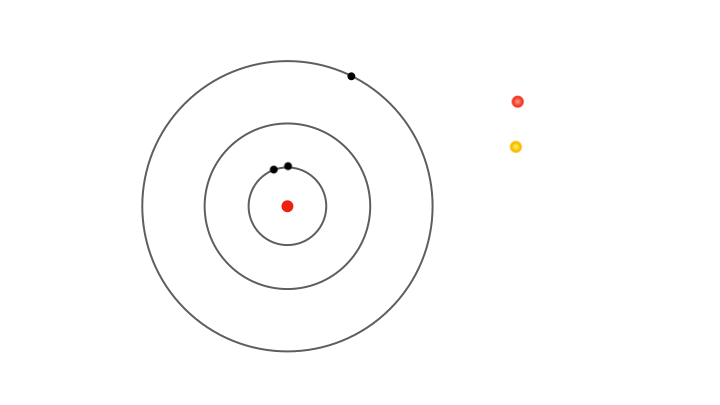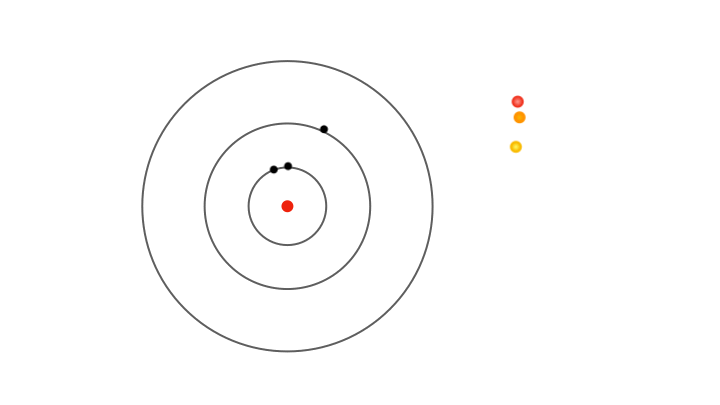
By stating that the electrons do not radiate, Bohr explained the stability of the atom. But in order to develop a concrete theory, he needed to match the movement of electrons within the atoms with the spectral lines observed. There was no doubt that the appearance of only specific coloured lines in a gas’s spectrum had to do with the electron energies inside atoms. Therefore, Bohr further postulated that electrons can orbit the nucleus without radiating only in specific orbits of fixed radii. Unlike the solar system where planets can orbit the Sun at any radius with the right velocity, electrons in Bohr’s model could occupy orbits of only certain, permitted radii.
Bohr’s next step was to precisely define the permitted radii. He fixed the values of electron angular momentum: electrons can only exist in orbits with an integer multiple of Planck’s constant as their angular momentum. This essentially provided Bohr with a method to assign the radii of the permitted orbits. Consequently, electrons in these allowed orbits could only possess specific permitted speeds.
For instance, an electron in the innermost orbit has the smallest possible radius, placing it closest to the nucleus. Bohr calculated this radius to be about 0.000000000053 metres — a millionth of the thickness of a human hair. In this orbit, the electron moves at about 2000 kilometres per second, completing around six thousand trillion revolutions around the nucleus each second. The next allowed orbit has a radius four times larger, with the electron moving at half the speed. Consequently, one can deduce the radii of all the permitted orbits and the corresponding electron speeds.
Electron energies
Due to the electron’s motion in each orbit as well as the electrical pull of the nucleus, the electron possesses some energy when confined to an allowed orbit. Since the radii and speeds of the electron vary discontinuously across the orbits, the electron’s energy also has discrete values—it varies in jumps rather than in a continuous manner. The energy is lowest in the innermost orbit and increases stepwise for outer orbits.
Yet fixed electron energies alone don’t explain why only specific colours appear in atomic spectra.. For this, Bohr proposed the concept of electrons jumping from one orbit to another. Whenever an electron jumps from an outer orbit to an inner one, it loses energy. This lost energy manifests has a pulse of radiation that has energy exactly equal to the lost energy, explaining why only certain colours appear in the atomic spectra. For instance, a jump from the second to the first orbit produces one spectral line, while jumps from higher orbits produce others.
So, it’s not the energies of electrons in allowed orbits that explain the discrete lines in the atomic spectra, but the differences in energy between orbits. Similarly, when radiation of suitable energy strikes an atom, an electron can absorb it and jump to a higher orbit. In terms of spectra, imagine passing white light through a gas, and using a diffraction grating to separate the light emerging on the other side, a continuous spectrum appears with dark lines where specific colours are missing. These missing colours correspond to the specific wavelengths of radiation absorbed by the electrons jumping to higher orbits.
Not the usual "jump"
It’s important to emphasize that when we imagine an electron “jumping” from one orbit to another, we shouldn’t picture it physically traveling between these orbits. An electron, in fact, only exists in specific, permitted orbits within the atom. So, how does it make the jump? One might imagine the electron vanishing from one orbit and reappearing in another, but such visualizations are simply mental aids. The true mechanism behind these jumps remains unknown. All we can reliably say is that the electron’s jump accounts for the discrete atomic spectra, and nothing more. It’s essential not to assume we know more than we actually do. As Bohr famously remarked, “We must be clear that, when it comes to atoms, language can be used only as in poetry. The poet, too, is not nearly so concerned with describing facts as with creating images and establishing mental connections.”
And so, Bohr’s atomic model based on his assumptions about electrons' orbits and jumps within atoms appears to accurately describe the atomic spectra. However, the theory only could explain the spectra of hydrogen gas and gases with hydrogen-like atoms with a single orbiting electron. Bohr was troubled by this limitation, and when he expressed reluctance to publish his findings, Rutherford reportedly encouraged him, saying that if it worked for hydrogen, people would believe the rest.
While Bohr’s atomic model wasn’t the final word on atomic structure, it was a crucial milestone towards a complete atomic theory, which was finally developed in the 1920s through collective efforts of young physicists like Heisenberg, Schrödinger, and Dirac, under the guidance of leaders like Bohr, Einstein, and Planck.
The quantisation of angular momentum proposed by Bohr mathematically is \[L=n{h\over 2\pi}\]
where \(n\) is any integer.
Using this rule along with the energy considerations of the orbiting electron in a hydrogen atom, we get the electron energy in the \(n^{th}\) orbit as \[E_n=-{13.6\over n^2}\,\mathrm{eV}\]
Hence, orbital energy of electrons is quantised too.


