Have you ever wondered how polarised sunglasses effectively reduce glare or how anti-glare filters in cameras can eliminate unwanted reflections from surfaces like water and glass? The answer lies in the nature of light waves and their transformation upon reflection.

In 1811, decades before the invention of polarised glasses, Scottish scientist Sir David Brewster formulated a law that describes how reflected light changes when it strikes a surface at a special angle, now known as Brewster’s angle. This law provides insights into various phenomena, such as why fish beneath the surface of a lake become visible when viewed through polaroid sunglasses, and how glare from sunlight reflected off roads can be significantly reduced with their use.

At the time of Brewster’s work, light was vaguely understood as a transverse wave—a type of wave where the oscillations are perpendicular to the direction of propagation. For example, if you fix one end of a string and move the other end up and down, a wave travels along the string’s length while parts of the string oscillate vertically. Similarly, if you move the string sideways instead, the oscillations occur horizontally. Light can also be thought of as a transverse wave with oscillations that can be constrained to a single direction. When this happens, the light is said to be polarised.

However, most natural sources of light including the Sun produce unpolarised light, where the oscillations occur in all possible directions perpendicular to the wave’s propagation. Imagine a bunch of strings laid parallel to each other, with different people moving their ends in random directions. The result is chaos with oscillations happening in all directions perpendicular to the wave. So, unpolarised light can be thought of as many polarised light waves stacked on top of each other, resulting in oscillations not confined to a single direction.

Polarising light

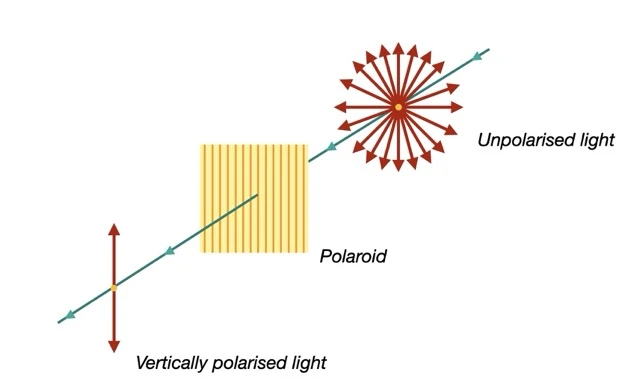
Unpolarised light can be converted into polarised light using a filter called a polaroid. Most polaroids are made from materials containing long molecules aligned in a single direction. These molecules allow electrons to move along their length, absorbing all oscillations parallel to the alignment. Light oscillating perpendicular to this direction, however, passes through largely unaffected. The result is polarised light. This principle is behind the working of polaroid sunglasses and windshields. By converting unpolarised light into polarised light, the intensity of the transmitted light is essentially halved, reducing glare and improving visibility.

When polarised light strikes a second polaroid the outcome depends on the alignment of the second filter. If its molecules are aligned parallel to the polarisation of the light, the light passes through. But if the polaroid is rotated 90 degrees, it blocks the light entirely. By placing two polaroids perpendicular to each other, unpolarised light can be completely blocked, as each stage reduces its intensity by half. This is in fact something you can test yourself with two polaroid sunglasses.

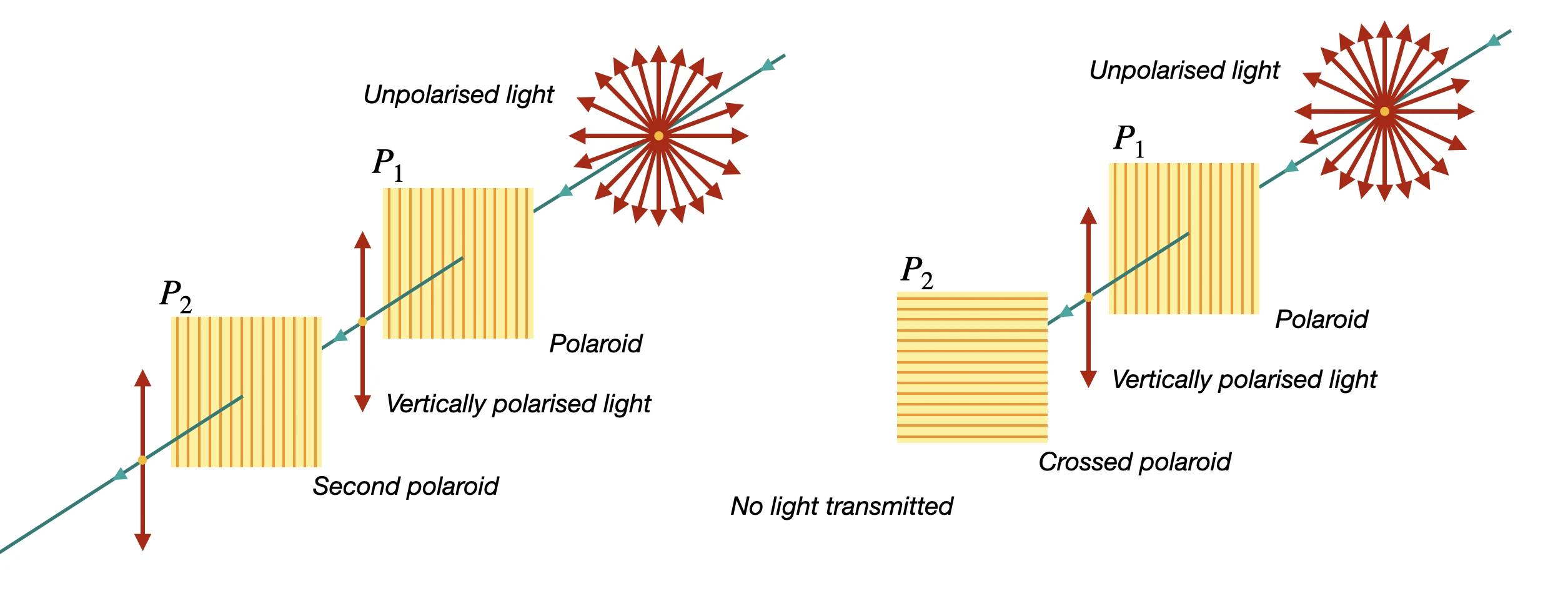
This concept was initially proposed to eliminate glare from headlights of oncoming cars—polarising filters would cover the headlights and windshields of cars. However, if the polaroid sheets are orientated perpendicular to each other, the light is completely blocked and the driver would be unable to see the oncoming cars! On the other hand, if the directions of the sheets are at different angles, the visibility of the road is significantly reduced, which can be hazardous in low-light conditions such as nighttime and when it’s cloudy.

Initial impressions

The first recorded observation that eventually inspired Brewster to investigate further and formulate a law was made by a French Army engineer, Etienne-Louis Malus. He observed sunlight reflecting off windows through a crystal that acted like a polaroid. Malus noticed that rotating the crystal caused variations in the intensity of the reflected light. He hypothesized that there was an unknown property of light that was causing this. He called this property “polarisation”.

To understand how Brewster investigated this phenomenon further, imagine a ray of polarised light striking a glass surface at an arbitrary angle. A portion of this light passes through the glass while the remainder reflects off its surface. The amount of light transmitted and reflected depends on the angle at which the light hits the surface. At a particular angle of incidence, which for glass is 56.3 degrees, no light is reflected, and all of it is transmitted into the glass. This specific angle of incidence is called the polarising angle, or commonly, the Brewster angle.

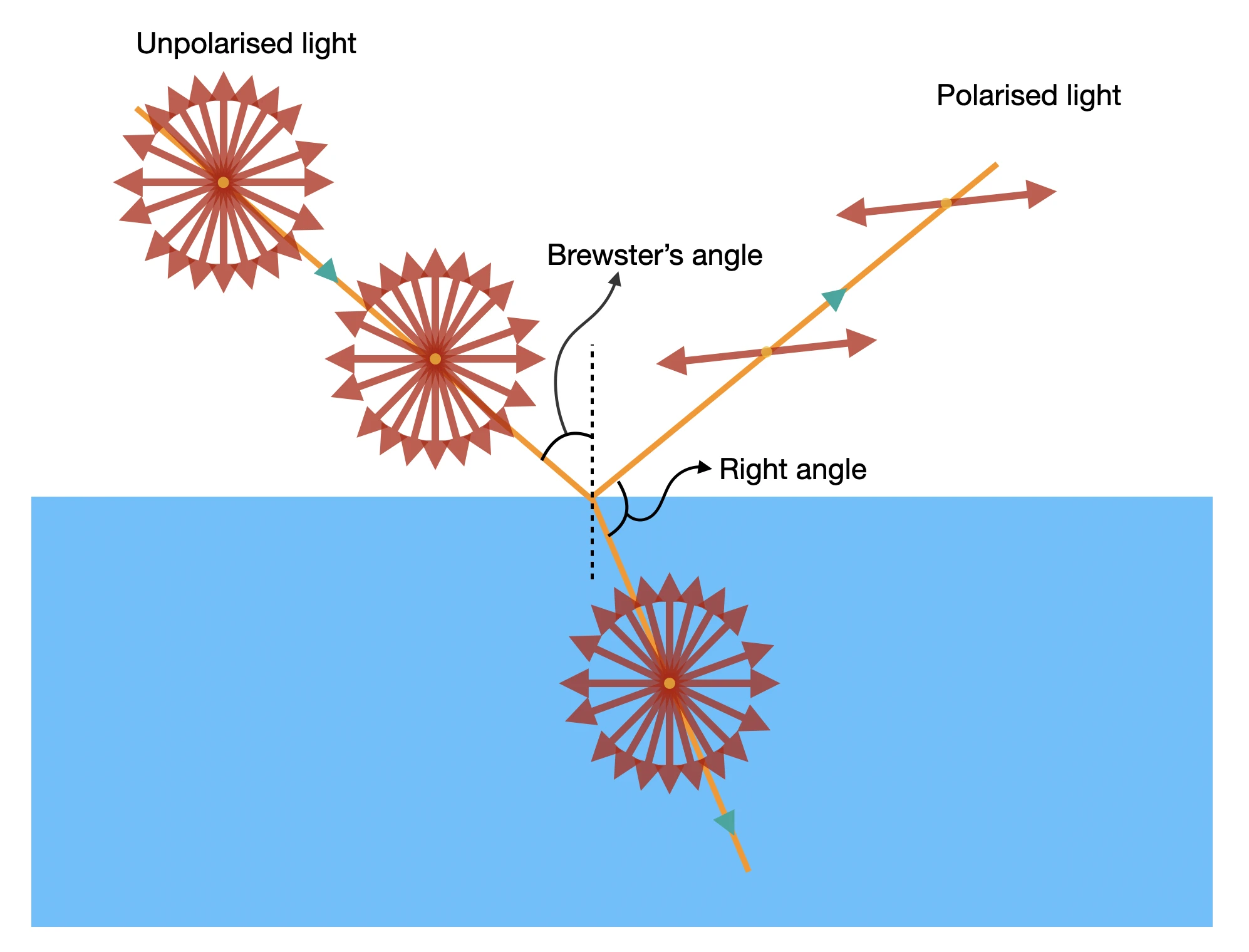
To truly grasp the phenomenon, imagine unpolarised light striking the glass surface. As before, some light is transmitted and some reflected. However, when the angle of incidence of the light on the glass matches the Brewster angle, the reflected light becomes completely polarised. We’ve essentially found a method of converting unpolarised light into polarised light without the need for a polaroid. Just ensure that the original unpolarised light strikes the glass at the polarising angle, and the reflected light will be polarised. The transmitted light however remains unpolarised.

Whether the reflected light is polarised can be easily determined by looking through a polaroid, as Malus inadvertently did. If the light is polarised, one of the orientations of the polaroid, aligned correctly with the long molecules, must completely block the light by absorbing it. However, Brewster’s original method of finding the polarising angle involved observing that when light is incident at the polarising angle, the reflected and transmitted lights form a right angle to each other. Hence, there are three things happening simultaneously—unpolarised light falling at the polarising angle, reflected light being completely polarised, and the reflected and transmitted lights forming a right angle. The occurrence of any one of these conditions implies the existence of the other two, for the considered set up.

Computing the speed of light

When Brewster repeated the experiments with different materials, including air, water, topaz, sulfur, diamond, and others, he discovered a deeper law at work. He found that the polarising angle depends on a property of the material the light is incident on, known as refractive index. The refractive index, in turn, depends on the speed of light in the material. Light travels fastest through vacuum at 300,000 km per second. But when it enters a different medium like glass, it slows down slightly, travelling at a speed of 200,000 km per second. This difference in speed allows us to compare the speeds of light in vacuum and glass. The refractive index of glass, which is 1.5, indicates that light travels 1.5 times slower in glass compared to vacuum

Brewster’s law provides a direct link between the polarising angle and a material’s refractive index. Specifically, the tangent of the polarising angle equals the refractive index. In essence, when unpolarised light strikes a material—such as glass—at precisely the polarising angle, the reflected light becomes completely polarised. This phenomenon enables us to calculate the material’s refractive index and, consequently, the speed of light within it. However, if the light hits the surface at any angle other than the polarising angle, the reflected light remains unpolarised, making it impossible to determine the speed of light in the material using this method.

If we repeated the same experiment using quartz instead of glass, we would observe a different polarising angle. Instead of 56.3 degrees observed for glass, the polarising angle for quartz would be 57.1 degrees. Hence, according to Brewster’s law, the refractive index of quartz is higher than that of glass. This means that light travels slightly slower in quartz compared to glass.

The legacy of Brewster’s law

Brewster’s law elegantly ties together three interconnected phenomena: light striking a material at specific angle, resulting in polarization of the reflected light, which in turn provides a way to calculate the material’s refractive index—a quantity linked to the speed of light within it. This principle underpins function of polaroid sunglasses.

Consider sunlight reflecting off a road. The reflected light becomes polarised, with vibrations confined to a direction parallel to the road’s surface. When this light passes through polarised lenses, the long molecular structures within the lenses absorb these horizontal vibrations, allowing only vertical ones to pass through. This drastically reduces glare while still maintaining a clear vision of the surroundings.

It’s interesting to note that such practical applications, which we often take for granted, were far from Etienne-Louis Malus’s thoughts when he first observed polarised light by casually rotating a crystal to view sunlight reflected off a window.